Highlight
Mathematical Models for Group Decision-Making
Achievement/Results
Our society has a long tradition of valuing the wisdom of groups. Groups offer the potential for redundancy and robustness, and are generally thought of as being more cautious, more creative, more informed, and more accurate than individuals. A large amount of previous work in various literatures has focused on the accuracy of groups in relatively specific situations; however, very little work has even mentioned group response time.
Researchers at the University of California, Santa Barbara have derived new and general mathematical results describing both the speed and accuracy of two families of group decision-making rules, and demonstrated how the results provide simple and intuitive ways to compare the performance of different potential group setups, ultimately informing the design of realistic decision-making systems. The research by Margot Kimura, a National Science Foundation (NSF) Integrative Graduate Education and Research Traineeship (IGERT) Fellow, and professor Jeff Moehlis at UC Santa Barbara extends the theoretical models found in group decision-making studies in areas including engineering, cognitive and social psychology, and economics.
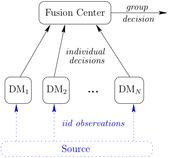
The goal of their decision-making system was to complete a two-alternative forced-choice (2AFC) task with no more than a specified level of (average) error, with additional desirable properties such as speed and robustness. In a 2AFC task, one must choose between two specific hypotheses while making the following three assumptions: (i) evidence favoring each alternative is integrated over time, (ii) the process providing the decision-makers with observations is subject to random fluctuations, and (iii) a decision is made when sufficient evidence favoring one of the alternatives has accumulated. There are many situations in which the sample size is not fixed in advance or when one wants to minimize the number of samples: for example, in ammunition quality control, tested samples are unusable; and in clinical trials, there is a moral obligation to use the minimal number of test subjects required to achieve the desired error rate. Wald and Wolfowitz proved in 1948 that the Sequential Probability Ratio Test (SPRT) solves a 2AFC task with the fewest (average) number of samples (equivalently, the fastest time); however, a decision-making system comprised of a single decision-maker is vulnerable to attack and/or failure. Because of this, the UC Santa Barbara team chose to exploit the power of groups to add additional desirable qualities to a decision-making system. While they originally intended for each group member to be modeled by the SPRT, they later found that the group models they developed were sufficiently general to accommodate any type of individual model.
In designing a group decision-making system, important considerations include the number of members in the group, whether to use a few sophisticated detectors or a large number of simple detectors, and how to incorporate at least one human observer into the system to provide accountability. In this NSF-funded project, the researchers addressed these considerations by developing methods to derive the group error rate and distribution of group decision times for an arbitrary number of independent and possibly non-identical decision-makers for three simple group decision rules: Race, where the fastest decision-maker sets the group’s decision; Majority Total, where the group waits until all of the decision-makers have answered, then applies a simple majority rule; and Majority First, a novel rule, where the group makes a decision as soon as the smallest possible majority agrees. The researchers then compared the performance of the schemes under different constraints, to determine the relative merits of each. Through the comparisons, the researchers determined that the Majority First scheme provided the best balance of speed, accuracy, and robustness in an uncertain situation: the scheme provides relatively quick decisions, provides a high level of accuracy, and is robust to a small number of sensors being hijacked or destroyed. The UC Santa Barbara team also derived results to provide the same level of detail for the natural generalizations of the Majority Total and Majority First schemes: in the eta-Total scheme, the group waits until eta decision-makers have decided, then applies a simple majority rule to those decisions; and in the eta-First scheme, the group selects the hypothesis that first gets eta votes, as soon as the (eta)th decision is made.
In summary, the models present a novel and general way in which one can intuitively yet mathematically model a group’s performance based on its members’ statistics, establish a reasonable base model which can be extended to build up more complicated models for realistic groups, and provide a means by which one can compare different group decision rules.
Address Goals
These results extend previous attempts to analytically describe the performance of a group in a sequential task using only the characteristics of its individual members in a simple and intuitive way. Unlike previous work, the results found in this research provide full descriptions of the group’s performance, rather than relying only on averaged values. Due to the general formulation of the solutions, these results apply to groups of humans, groups of sensors, or a cybernetic group comprised of both. Moreover, the results naturally extend to hierarchical and more complicated group topologies in which some “members” are groups.
Another positive result from this work is the experience it gave graduate student Margot Kimura in identifying and solving problems of fundamental and practical interest. This contributes to the NSF’s goal of fostering a highly skilled scientific and engineering workforce.